მსხვერპლის მიერ მტაცებლების საწინააღმდეგოდ შექმნილი ადაპტაციები ხელს უწყობს მტაცებლების მექანიზმების შემუშავებას ამ ადაპტაციების დასაძლევად. მტაცებლებისა და დაზარალებულთა გრძელი თანაცხოვრება იწვევს ურთიერთქმედების სისტემის ჩამოყალიბებას, რომლის დროსაც ორივე ჯგუფი სტაბილურად არის დაცული სასწავლო ზონაში. ასეთი სისტემის დარღვევა ხშირად იწვევს გარემოზე უარყოფით შედეგებს.

კო-ევოლუციური ურთიერთობების დარღვევის უარყოფითი გავლენა შეინიშნება სახეობების შემოღების დროს. კერძოდ, ავსტრალიაში შემოღებულ თხებსა და კურდღლებს ამ კონტინენტზე არ გააჩნიათ უხვი კონტროლის მექანიზმები, რაც იწვევს ბუნებრივი ეკოსისტემების განადგურებას.

მათემატიკური მოდელი

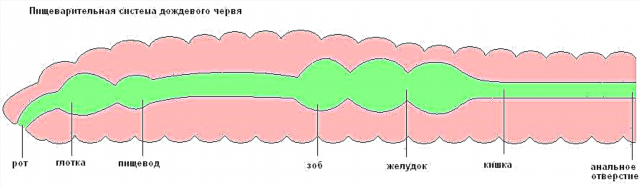
დავუშვათ, რომ ცხოველთა ორი სახეობა ბინადრობს გარკვეულ ტერიტორიაზე: კურდღელი (მცენარეებით კვება) და მელა (კურდღლებზე კვება). მოდით კურდღლების რაოდენობა x < displaystyle x>, მელაების რაოდენობა <<displaystyle y>. მალტუსის მოდელის გამოყენებით აუცილებელი ცვლილებებით, მელაების მიერ კურდღლების ჭამის გათვალისწინებით, ჩვენ ჩამოვალთ შემდეგ სისტემაში, რომელსაც ეკისრება Volterra მოდელის სახელი - უჯრები:

<x ˙ = (α - c y) x, y ˙ = (- β + d x) y. < displaystyle < დაიწყოს< წერტილი > = ( alpha -cy) x, < წერტილი > = (- ბეტა + dx) y. ბოლოს>>

ამ სისტემას აქვს წონასწორობის მდგომარეობა, როდესაც კურდღლებისა და მელაების რაოდენობა მუდმივია. ამ მდგომარეობიდან გადახრა იწვევს კურდღლებისა და მელაების რაოდენობის რყევას, ჰარმონიული ოსტატორის რყევების მსგავსი. როგორც ჰარმონიული ოსტატორის შემთხვევაში, ეს ქცევა სტრუქტურულად არ არის სტაბილური: მოდელის მცირე ცვლილებამ (მაგალითად, კურდღლების საჭირო რესურსების გათვალისწინებით) შეიძლება გამოიწვიოს ქცევის თვისებრივ ცვლილებას. მაგალითად, წონასწორობის მდგომარეობა შეიძლება გახდეს სტაბილური, ხოლო რიცხვების რყევება გაფუჭდება. საპირისპირო სიტუაცია ასევე შესაძლებელია, როდესაც წონასწორობის პოზიციიდან ნებისმიერი მცირე გადახრა გამოიწვევს კატასტროფულ შედეგებს, ერთ – ერთი სახეობის სრულ გადაშენებამდე. კითხვაზე, თუ რომელია ამ სცენარების დანერგვა, Volterra-Tray მოდელი არ იძლევა პასუხს: აქ საჭიროა დამატებითი გამოკვლევა.

რხევების თეორიის თვალსაზრისით, ვოლტერა - ლოტკას მოდელი არის კონსერვატიული სისტემა, მოძრაობის პირველი ინტეგრალით. ეს სისტემა არ არის ნედლი, რადგან განტოლებათა მარჯვენა მხარეს მცირედი ცვლილებები იწვევს მის დინამიკურ ქცევაში თვისებრივ ცვლილებებს. ამასთან, შესაძლებელია ”ოდნავ” მოდიფიცირება განტოლების მარჯვენა მხარის ისე, რომ სისტემა გახდეს თვითწერილი. სტაბილური ლიმიტის ციკლის არსებობა, რომელიც თან ახლავს უხეში დინამიური სისტემების არსებობას, ხელს უწყობს მოდელის მოქმედების ველის მნიშვნელოვან გაფართოებას.

მოდელის ქცევა

მტაცებლებისა და მათი მსხვერპლის ჯგუფური ცხოვრების წესი რადიკალურად ცვლის მოდელის ქცევას, აძლიერებს მას სტაბილურობას.

დასაბუთება: ჯგუფური ცხოვრების წესის მიხედვით, მტაცებლების პოტენციური მსხვერპლის შემთხვევითი შეტევების სიხშირე მცირდება, რაც დასტურდება სერენგეთის პარკში ლომებისა და მხეცების რაოდენობის დინამიკის დაკვირვებით.

მოთხრობა

"მტაცებელი - მტაცებელი" ტიპის ორი ბიოლოგიური სახეობის (პოპულაცია) თანაცხოვრების მოდელს ასევე უწოდებენ ვოლტერა - ლოტკას მოდელს.

ის პირველად მიიღო ალფრედ ლოტკამ 1925 წელს (გამოიყენებოდა ბიოლოგიურ პოპულაციათა ურთიერთქმედების დინამიკის აღწერა).

1926 წელს (ლოტკის მიუხედავად) მსგავსი (და უფრო რთული) მოდელები შეიმუშავა იტალიელმა მათემატიკოსმა ვიტო ვოლტერამ. მისმა სიღრმისეულმა კვლევებმა გარემოსდაცვითი პრობლემების სფეროში, საფუძველი ჩაუყარა ბიოლოგიურ საზოგადოებათა მათემატიკურ თეორიას (მათემატიკური ეკოლოგია).